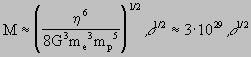NANE BIANCHE

NANE BIANCHE E NEBULOSE PLANETARIE
di Oriano Spazzoli

SOMMARIO:

Nane bianche

Come abbiamo visto una stella nella parte finale della sua vita perde materia per effetto di forti venti stellari, accentuati dal fatto che, essendo aumentato il raggio, la gravità superficiale della stella si è ridotta. L’astrofisico indiano S. Chandraseckar calcolò una massa limite al di sotto della quale i residui stellari, quando le reazioni termonucleari non sono più abbastanza efficienti per mantenerli in equilibrio idrostatico, proseguono la loro contrazione piuttosto lentamente finché non raggiungono una nuova condizione di equilibrio, garantita però non più dall’energia prodotta dalle reazioni termonucleari, bensì dal comportamento statistico della materia elementare quando viene sottoposta a densità elevate, quali sono quelle che si verificano nelle regioni centrali delle stelle alla fine della loro vita.

Le densità medie alle quali si creano queste condizioni sono dell’ordine di grandezza di 10^⁶ g/cm^³, per temperature intorno ai 100.000 °K. Ma che cosa accade e quali proprietà della materia emergono in tali condizioni ?

La risposta viene fornita anche in questo caso dalle conoscenze del comportamento delle particelle elementari, e in particolare degli elettroni; gli elettroni, lo ricordiamo, sono i portatori di carica negativa che si occupano la parte esterna dell’atomo, suddivisi in strati a ciascuno dei quali corrisponde un dato livello energetico (naturalmente con energia crescente al crescere della distanza dal nucleo). Il grande fisico teorico svizzero W. Pauli fu il primo a ipotizzare che gli elettroni occupassero i loro livelli energetici rispettando una legge ben precisa: “due elettroni in un atomo non possono occupare lo stesso stato”. Questo spiegò perché, nonostante un qualunque sistema fisico tenda ad assumere tra tutti i possibili stati, quello a minima energia, gli atomi nello stato fondamentale contengano elettroni a diversi livelli energetici e non tutti gli elettroni si trovino ammucchiati al minimo livello energetico. Ancor di più questa ipotesi rendeva conto del motivo per cui, all’aumentare del numero atomico non diminuisse regolarmente il raggio atomico e non aumentasse altrettanto costantemente l’energia necessaria per ionizzare l’atomo (comportamenti che ci si aspettava che accadessero dal momento che l’aumentare del numero di protoni avrebbe determinato l’aumento dell’attrazione elettrostatica del nucleo sugli stessi elettroni). La impossibilità per due particelle appartenenti ad un dato sistema (ad un gas di particelle) di occupare lo stesso stato è denominato “principio di esclusione”. Per il principio di esclusione, un gas di particelle che obbediscono ad esso (giacché non tutte vi obbediscono) può venire compresso soltanto fino a una densità limite alla quale le particelle occupano il minimo spazio ad esse concesso in ragione del loro moto. A tale densità la pressione non dipende più dalla temperatura, come per i nostri gas nelle condizioni standard (il cui comportamento è esaurientemente descritto dalla legge dei gas perfetti
P.V = nRT ed è assai sensibile alla temperatura), ma dipende unicamente da quanto esse sono state compresse. Infatti la conformità del loro comportamento statistico al principio di esclusione (impossibilità fisica di occupare lo stesso stato, lo ricordo) determina una resistenza alla compressione, sotto forma di pressione esercitata verso l’esterno, che aumenta con l’aumentare della densità secondo la legge .

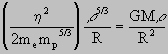
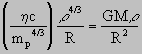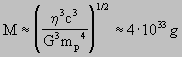La materia in queste condizioni è detta “degenere”; un gas degenere di elettroni liberi è un sistema “ordinato” nel quale le particelle occupano tutti gli stati possibili al di sotto di un certo valore limite dell’energia, detto “energia di Fermi”, o “livello di Fermi”, come se il pubblico nella platea di una sala cinematografica si fosse disposto tutto quanto nelle prime file senza lasciare in esse alcun posto vuoto, invece di disporsi a caso, sparso per tutta la sala (gas ideale, descritto dalla termodinamica e dalla meccanica statistica classica).

Si veda a questo proposito nell’appendice 1 una descrizione più dettagliata delle condizioni fisiche del gas di elettroni degeneri.

Poiché dunque la materia stellare diventa una specie di pasta compatta di elettroni degeneri (con in mezzo i nuclei come l’uva passa nel panettone) ad elevate densità, eserciterà una forte pressione verso l’esterno che, se la massa complessiva della struttura stellare non è troppo elevata, equilibrerà la gravità; si realizza quindi una condizione di equilibrio idrostatico, non garantito però dalla pressione del gas riscaldato da alcuna fonte di energia, bensì dalla pressione degli elettroni degeneri determinata dal principio di esclusione.

Tuttavia abbiamo usato l’espressione “se la massa non è troppo elevata”; infatti con l’aumentare della massa, la densità nella regione centrale di una stella aumenta, e all’aumentare di essa aumenta l’energia massima degli elettroni. Per masse superiori al valore limite di 1,5 masse solari (limite di Chandraseckar) essi divengono relativistici (l’energia di Fermi è molto superiore alla loro energia a riposo), e quando ciò accade (si vedano le appendici 1 e 2 per una spiegazione fisica), la pressione del gas degenere, al crescere della densità cresce più lentamente () e non riesce più a bilanciare la gravità e la contrazione della stella prosegue assumendo le caratteristiche di una implosione, il “collasso gravitazionale”. In effetti la quantità di moto aumenta con l’aumentare di densità per il principio di esclusione, ma la materia non può superare la velocità della luce, quindi quantità di moto ed energia non sono più legate alla velocità dalle relazioni note della meccanica classica, ma il loro aumento è dovuto unicamente all’aumento della massa relativistica; ne segue che la pressione non è più sensibile all’aumento della densità come nel caso precedente.

Struttura interna e parametri fisici delle nane bianche

Le simulazioni al calcolatore di nane bianche ci forniscono un quadro che possiamo schematizzare semplicemente in questo modo:

un nucleo centrale degenere nel quale si trovano gli elementi più pesanti,
uno strato intermedio di elio inerte,
uno strato superficiale di idrogeno.

In talune nane bianche l’idrogeno risulta completamente assente; esse vengono indicate con la sigla DB, per distinguerle dalle nane con idrogeno, che vengono indicate con DA.

L’esistenza delle nane bianche di tipo DB si deve a due possibili cause:

la perdita dell’idrogeno in superficie a causa dei forti venti stellari che caratterizzano la fase finale della vita della gigante rossa da cui la nana si forma,
la fusione dell’idrogeno che prosegue nell’involucro durante la fase di contrazione lenta che porta alla formazione della nana.

In condizioni di stabilità una nana bianca ha temperatura superficiale di circa 100.000 °K; la densità all’interno è quella tipica della materia in condizioni di degenerazione degli elettroni, cioè circa 10^⁶ g/cm^³. A densità di questo tipo una stella come il Sole risulterebbe avere un raggio di soli 10.000 chilometri (sarebbe in pratica poco più grande della Terra).

Naturalmente la nana bianca, mentre tende a raggiungere le condizioni di stabilità, proseguendo il suo processo di contrazione lenta, aumenta la sua temperatura superficiale. Per questo motivo ci dovremmo aspettare di vedere nane bianche in evoluzione distribuite più o meno uniformemente su di un intervallo di temperature che va da 10-15.000 °K fino a 100.000 °K circa; al contrario mancano nane bianche con temperature tra 30.000 e 45.000 °K e se ne ignora il motivo.

Nane bianche e nebulose planetarie

In una gigante rossa nel “ramo asintotico” del diagramma HR, alla fine della sua vita, la contrazione della parte interna, che diviene la nana bianca, si accompagna alla perdita dell’involucro gassoso, più denso all’interno perché la perdita di materia dalla superficie della stella è cresciuta con l’aumentare della luminosità. Quando la temperatura superficiale della stella centrale è salita a 30.000 °K, l’emissione ultravioletta diventa tale da determinare la ionizzazione del gas circostante, residuo dell’involucro della gigante originaria, espulso. La fluorescenza (prodotta dalla ricombinazione degli atomi del gas) determina il fenomeno delle nebulose planetarie: gli spettri a righe di emissione delle nebulose planetarie (osservati per la prima volta da W. Huggins nel 1864) contengono naturalmente in prevalenza righe dell’idrogeno, ma anche righe di elio, azoto, neon, ossigeno e ossigeno ionizzato (queste ultime poi, osservate per la prima volta da Huggins nel XIX, quando ancora non si aveva alcuna conoscenza della struttura atomica furono spacciate per righe di un nuovo elemento sconosciuto, che fu denominato “Nebulio”).

Il nome “nebulose planetarie” fu attribuito a questi oggetti fin da quando, nel XVIII secolo William Herschel le osservò per la prima volta, e le vide come tenui dischi simili ai pianeti.

Una nebulosa planetaria si espande in modo che dopo circa 10.000 anni le sue dimensioni sono divenute di 0,5 anni luce e dopo 50.000 anni si è dispersa nello spazio.

Recenti osservazioni con lo Hubble Space Telescope, hanno rivelato una spettacolare varietà di forme, che si cerca di spiegare con le interazioni dinamiche dei venti stellari (in seguito ai quali la gigante perde materia nella fase finale della sua vita) tra di loro e con il mezzo interstellare. Se i forti venti stellari per le giganti rosse si spiegano con l’aumento del raggio stellare e quindi con la diminuita gravità superficiale, naturalmente per lo stesso motivo le nane bianche dovrebbero perdere quantità minime di materia avendo una elevata densità e quindi certamente una elevata gravità superficiale; eppure si valuta che dalla loro superficie possa essere emesso un vento a bassa densità, ma anche ad alta velocità di uscita (naturalmente perché la velocità di fuga dalla superficie è aumentata essendo più elevata la gravità superficiale), detto “vento veloce” (la sua velocità è di qualche migliaio di Km/s) per distinguerlo dal vento principale, che è quello che provoca la perdita dell’inviluppo stellare e che è chiamato “supervento”, la cui velocità è di qualche decina di Km/s.

Quando l’inviluppo gassoso, durante la sua fase di espansione che dà origine alla nebulosa planetaria, si raffredda gli atomi di gas cominciano ad aggregarsi in gruppi molecolari. Quando la temperatura è scesa al di sotto di 1.000 gradi cominciano a formarsi granuli di polvere, per lo stesso motivo fisico (la tendenza delle molecole ad aggregarsi in corpuscoli al calare della temperatura) per cui nei nostri comuni processi di combustione si formano particelle di fumo; questi formano una nube che avvolgendo il residuo stellare ne diffonde la radiazione fino a renderlo invisibile. Nubi di polvere di questo tipo sono state rivelate da IRAS (Infra-Red Astronomical Survey), sigla con la quale venne denominato il sistema di sensori a raggi infrarossi che a bordo di un satellite registrò l’emissione infrarossa dallo spazio e scoprì numerose sorgenti emittenti radiazione di questa banda di frequenze; sorgenti avvolte in nubi di polvere sono rilevabili nell’infrarosso perché la polvere, i cui grani hanno dimensioni medie di 1 micron (un milionesimo di metro), diffonde in maniera consistente la luce di lunghezza d’onda minore delle dimensioni delle sue particelle, mentre rimane pressappoco trasparente a lunghezze d’onda superiori (tra le quali, appunto, quelle della banda infrarossa).

Nane bianche in sistemi binari: le stelle novae

In un sistema di binarie strette la stella più massiccia, anche se perde parte della materia del suo inviluppo esterno, la quale a sua volta va ad arricchire di idrogeno la compagna, si evolve in maniera più rapida e, se la sua massa è minore del limite di Chandraseckar, diviene una nana bianca.

Sappiamo che una nana bianca ha una elevata gravità superficiale, e perciò la materia che con la sua attrazione gravitazionale riesce a strappare alla compagna, cadendo sulla sua superficie acquista velocità ed energia elevate. Inoltre questo gas è dotato di un momento angolare (in termini non tecnici, diciamo che ha una rotazione) rispetto alla nana bianca, e per questo motivo non cade su di essa lungo un percorso rettilineo, ma mantiene tale rotazione ammassandosi su di un “disco di accrescimento”, nel quale attriti interni e perdite per irraggiamento la impoveriscono di energia favorendone la caduta a spirale sulla superficie dell’oggetto compatto. Il disco di accrescimento aumenta di dimensioni fino a raggiungere uno stato di equilibrio nel quale il flusso in entrata della materia è uguale a quello di uscita del gas in caduta.

L’aumento di temperatura e di densità in seguito all’accumulazione di idrogeno nello strato superficiale della nana bianca, produce l’innesco della reazione di fusione dell’idrogeno nello strato stesso; l’energia sviluppata in questo processo viene liberata improvvisamente in una esplosione che fa aumentare la luminosità della stella di un fattore 10^{^3~4} e talvolta anche superiore. Questo processo esplosivo però non disgrega la nana bianca, ma ne ripristina le condizioni di quiescenza iniziali e questo fenomeno è con ogni probabilità all’origine del comportamento delle cosiddette “novae ricorrenti”, nelle quali le esplosioni sono periodiche.

Oscillazioni della luminosità di minore entità e a breve periodo sono probabilmente prodotte dal fatto che l’impatto della materia risucchiata alla compagna, cadendo sul disco lo riscalda nel punto dell’impatto, e che la rotazione del sistema produce eclissi periodiche della “macchia calda” (hot spot) prodotta dall’impatto.

Può accadere anche che nella caduta del gas sulla superficie dal disco di accrescimento venga irraggiata radiazione ultravioletta che ionizza il gas circostante producendo una emissione a fluorescenza che ricorda per spettro e caratteristiche fisiche quella delle nebulose planetarie, anche se gli oggetti nebulari che la emettono hanno forme molto più irregolari.

Gli spettri delle novae durante la fase di quiescenza sono continui e corrispondenti ad una elevata temperatura superficiale; la luminosità assoluta in tale fase è molto bassa, ed essendo essa legata alla temperatura dalla relazione nota , se ne deduce che il raggio R delle stelle in questione è molto piccolo. È da questo tipo di considerazioni che si è attribuita l’origine del fenomeno delle novae alle nane bianche o a stelle avviate a diventarlo.

La fase esplosiva è invece caratterizzata da variazioni dello spettro, che forniscono indicazioni sulle modalità dell’esplosione:

una prima fase nella quale lo spettro è un continuo di tipo stellare, con righe di assorbimento allargate per l’elevata temperatura del gas e fortemente spostate a causa della sua elevata velocità di espansione, impressa ad essa dal processo esplosivo;
una seconda fase nella quale lo spettro è a righe inizialmente sovrapposte al continuo dell’involucro gassoso espulso, ma che gradualmente, quando il gas diviene rarefatto, divengono l’elemento dominante dello spettro;
successivamente, all’indebolirsi delle righe, comincia ad essere visibile il debole continuo della nana bianca nella fase di quiescenza.

Queste variazioni sono perfettamente compatibili con l’ipotesi che il fenomeno sia appunto un processo esplosivo nel quale la stella dapprima scaglia fuori un guscio di materia che forma un’onda d’urto sferica, la quale poi diradandosi genera una piccola nebulosa.

Appendice 1

Equazioni di stato della materia degenere

Si può esprimere facilmente l’energia di Fermi in funzione della densità di un gas degenere: sappiamo infatti che per il principio di indeterminazione:

D x × D p » h

dove h = h/2p, h = 6,6^.10^{^-34} joule×sec è la costante di Planck, D x è l’indeterminazione della posizione, cioè la semi-ampiezza dell’intervallo delle possibili posizioni x della particella, e D p è l’indeterminazione della quantità di moto lungo la stessa direzione.

e, poiché in un sistema che dovrebbe occupare il minimo spazio possibile le particelle dovrebbero essere ferme, l’indeterminazione D p dovrebbe essere anche il valore massimo di p, cioè:

(che indichiamo con, dove la F sta per Fermi, e che si indica con “quantità di moto di Fermi”). Poiché, inoltre, l’energia è legata alla quantità di moto dalla nota relazione

e la densità è:

(dove è il volume di un cubo di spigolo D x, e si può considerare il volume di una cella elementare occupata dall’elettrone), sostituendo la (1) e la (3) nella (2) si ottiene

Sappiamo poi che la teoria cinetica dei gas lega l’energia delle singole particelle alle grandezze termodinamiche temperatura T e pressione P; in particolare dalla relazione esistente tra la pressione e l’energia media di una particella segue la relazione

Poiché la densità numerica n è legata alla densità di massa r dalla relazione, (dove m_pè la massa di un protone), segue che

che significa appunto che la pressione della materia degenere dipende soltanto dalla densità.

Quando poi la densità è tale da produrre energie di fermi relativistiche (, dove è l’energia a riposo della particella), cambia la relazione che lega l’energia alla quantità di moto; infatti secondo la dinamica relativistica, energia e quantità di moto sono rispettivamente:

ed il loro rapporto è pertanto:

Per particelle altamente relativistiche (), si ha che:

allora la legge che lega l’energia di Fermi alla densità risulta:

e la legge della pressione (7):

Appendice 2

Equilibrio idrostatico e materia degenere

Sappiamo che l’equilibrio idrostatico è tra la forza gravitazionale e la forza determinata dalla pressione; naturalmente un elemento di materia di massa D m sente una forza di pressione in una data direzione se la pressione (cioè la forza che agisce sull’unità di superficie) subisce una variazione in quella direzione, e per questo la pressione da una parte dell’elemento è maggiore di quella dalla parte opposta lungo la direzione data. Se con F indichiamo la forza di pressione netta agente sull’elemento di materia, con D P=F/S indichiamo la differenza di pressione che determina la spinta netta, dove S è la superficie della faccia che l’elemento rivolge perpendicolarmente alla direzione data, e con D R indichiamo la sua lunghezza nella direzione considerata, in modo che il rapporto

D P/D R=F/(S× D R)

diventa la forza di pressione che agisce sull’unità di volume (il volume dell’elemento di materia risulta infatti:

D V=S× D R).

In condizioni di equilibrio idrostatico la forza di pressione sull’unità di volume è bilanciata dalla forza di gravità sull’unità di volume, cioè da:

Eguagliando le due espressioni della forza sull’unità di volume si ottiene l’equazione dell’equilibrio idrostatico:

(o in forma differenziale ).

Sostituendo D P e D R con P e R per semplicità, indicando con la densità media e applicando le due diverse equazioni di stato della materia degenere, si ottiene una relazione tra la massa e la densità media di una nana bianca in entrambi i casi.

Nel caso non relativistico () si ottiene la relazione:

,

dalla quale si ottiene, applicando la legge della densità e ricavando la massa in funzione di r,

il che sta a indicare che la densità media (e quindi quella centrale) cresce al crescere della massa della nana bianca, ma anche che, una stella di elettroni degeneri non relativistici può essere stabile per diversi valori della sua massa.

Nel caso relativistico al contrario, l’applicazione dell’equazione di stato all’equazione dell’equilibrio idrostatico non produce alcuna dipendenza della massa stessa dalla densità; ciò indica che una nana bianca degenere stabile può esistere soltanto per un valore critico della massa, e che oltre quella massa critica non può più esserci stabilità. Possiamo stimare la densità critica semplicemente eguagliando le due leggi dell’energia di Fermi nei due casi relativistico e non relativistico:

da cui, calcolando n, segue:

che rappresenta la densità numerica degli elettroni in una fase di transizione da gas non relativistico a gas relativistico. Poiché la stella è neutra, a ogni elettrone corrisponderà un protone, quindi per ottenere la densità di materia, basterà moltiplicare n per la massa di un protone, in modo da ottenere:

Se allora, come abbiamo visto, la densità di una nana bianca cresce al crescere della massa secondo la legge (11), e la densità critica viene raggiunta ad una massa critica al di sopra della quale la stella non riesce più a raggiungere una condizione di equilibrio idrostatico, possiamo anche stimare l’ordine di grandezza della massa critica calcolandola dall’equazione dell’equilibrio idrostatico semplificata (già usata nel caso non relativistico) nel caso di materia degenere relativistica; ne segue che

e, se si esprime il raggio in funzione della massa e della densità (applicando la legge della densità ), ricavando la massa si ottiene l’espressione approssimata:

che è circa il doppio della massa del Sole. In realtà, con un calcolo esatto (e senza ignorare le costanti numeriche) il limite di Chandraseckar risulta essere poco superiore:

Singolare è poi la deduzione che si può fare dalla relazione (10); poiché essa può anche essere scritta

sostituendo a r la sua legge, si ricava:

e successivamente da semplici calcoli algebrici:

da cui, elevando al quadrato entrambi i membri

In altre parole, all’aumentare della massa di una nana bianca diminuisce il suo raggio.

Appendice 3

Massa minima di una nana bianca e massa di un pianeta

Dalla equazione semplificata dell’equilibrio idrostatico nelle condizioni di un gas di elettroni degeneri non relativistici, applicando la legge della pressione di degenerazione, si ottiene una espressione della massa di un corpo di materia degenere:

La dipendenza della massa dalla densità è tipica delle stelle degeneri; per i corpi celesti a bassa temperatura, come i pianeti, tale legge non vale più. Sappiamo infatti come i pianeti solidi, o “rocciosi”, pur avendo masse diverse tra loro, hanno densità distribuite in un intervallo di valori piuttosto stretto (intorno a 5g/cm^³).

Si può calcolare la densità tipica di un corpo freddo dividendo la massa di un protone per una stima tipica del volume di un atomo di idrogeno (, dove è il raggio di Bohr);

il valore così ottenuto è di circa:

Sostituendo tale densità nell’equazione (19) si ottiene una massa che può essere considerata limite superiore per un pianeta e limite inferiore per una nana bianca:

Monografia n.63-2001/6

Torna alla Home Page di Testi & Trattati