di Oriano Spazzoli

di Oriano Spazzoli
«Gli astronomi devono essere cosmopoliti perché non ci si può attendere che uomini di stato ignoranti apprezzino i loro servigi.» (Tyge Brahe)
Introduzione.
Quando nel 1543 fu pubblicato il “De rivolutionibus orbium coelestium”, il trattato astronomico di Niccolò Copernico nel quale egli tracciava per la prima volta le ragioni astronomiche del modello cosmologico eliocentrico, spiegando come, con maggior semplicità esso potesse spiegare il moto retrogrado dei pianeti nella volta celeste.
Ma la guerra della “Nuova Scienza” contro la filosofia naturale degli aristotelici, le cui idee fondamentali confluivano nella cosmologia geocentrica, non era ancora vinta; sono testimonianza di ciò i toni della prefazione successivamente all’opera dal teologo Osiander, nella quale viene evidenziato il carattere di puro esercizio astronomico e geometrico dell’opera, che egli invece considera priva di valore dal punto di vista astronomico. Occorrevano ancora solide prove fisiche che sostenessero la teoria eliocentrica, anche perché il tentativo di Copernico di conciliarla con la fisica di Aristotele era stato pieno di contraddizioni e poco credibile.
Tale compito fu assolto anzitutto da Galileo Galilei, il quale modificando il metodo sperimentale attraverso l’introduzione del linguaggio matematico nella descrizione dei fenomeni e delle leggi, dimostrò come a ormai duemila anni di distanza dalla prima formulazione dei principi della fisica aristotelica, il mondo fosse maturo per il loro superamento. D’altra parte la strada dell’osservazione sistematica si era cominciata a battere già dal XV secolo, da quando cioè il patrizio tedesco Bernhard Walther per primo, seguito poi da molti altri, cominciò a utilizzare l’osservazione del cielo non più come una operazione da svolgere episodicamente, soltanto per correggere un parametro della teoria preesistente, ma come una pratica da svolgere con regolarità e competenze professionali specifiche (egli fu forse il primo astronomo che utilizzò l’orologio per registrare i tempi delle osservazioni).
Le sue osservazioni furono poi pubblicate un anno dopo il “De Rivolutionibus”, da Johannes Shoener, astronomo e matematico contemporaneo di Copernico. Indiscutibilmente, tuttavia, il maggiore sostegno al modello eliocentrico per quanto riguarda l’osservazione dei moti planetari e per quanto riguarda la loro formulazione cinematica, fu fornito da due grandi personaggi, che espressero il loro genio proprio nei due campi suddetti, e che incontrandosi e unendo le loro esperienze realizzarono uno dei più evidenti casi di connessione sequenziale tra osservazione e teoria che la storia della scienza ricordi: essi furono l’astronomo Tycho Brahe e l’astronomo e matematico Johannes Kepler.
Il destino volle che i 25 anni che divisero la loro nascita, abbiano permesso a Tycho, più vecchio (nacque nel 1546 a Knudstrup in Scania, oggi in Svezia, allora in Danimarca) ed esperto osservatore, di raccogliere un numero di dati sufficienti a permettere a Keplero, matematico assai più brillante, di giungere a conclusioni che rafforzavano ancora di più il modello cosmologico eliocentrico.
Tycho: gli studi e le prime osservazioni
Nato, come già detto, in Danimarca, da famiglia patrizia (il padre era governatore del castello di Helsingborg, di fronte al castello di Helsinore, ove si svolge la vicenda dell’Amleto di Shakespeare), Tyge (Tycho è la latinizzazione del suo nome vero) Brahe venne affidato fin dall’infanzia allo zio Joergen Brahe, viceammiraglio, nella cui tenuta di campagna apprese i primi rudimenti di Latino a sette anni. A tredici anni lo zio iscrisse il giovane Tycho all’Università di Copenaghen, ove studiò Filosofia e Retorica senza troppo entusiasmo.
Dopo i tre anni canonici all’Università, Tycho fu mandato a Lipsia, a perfezionare la sua educazione che attraverso il suo percorso di studi doveva condurlo a dedicarsi alla carriera diplomatica. Lo accompagnava un tutore appena ventenne (il futuro storico Anders Soerensen Vedel) che aveva il compito di impedirgli di coltivare la passione per il cielo, forse nata in lui dall’osservazione di un eclisse totale di Sole il 21 Agosto del 1560, e per la quale portò con sé un piccolo globo celeste comprato poco tempo prima della partenza. Negli anni seguenti, trascorsi in peregrinazioni tra Lipsia, Rostock, Basilea e Augusta, Tycho acquistò efemeridi e tavole astronomiche (dalle antiche “Tavole Alfonsine” fino alle più recenti “Tavole prussiane”, pubblicate da Erasmus Reinholds nel 1551), e cominciò ad effettuare le prime misure astronomiche (la prima all’età di diciassette anni, quando misurò la distanza tra Giove e Saturno in occasione di un loro avvicinamento, previsto con in base alle Tavole Alfonsine in anticipo di circa un mese, mentre le più recenti Tavole prussiane, basate sul modello copernicano, ne prevedevano il verificarsi con soltanto qualche giorno di anticipo).
Nel 1964 Tycho acquistò una “balle-strigia” (strumento utilizzato per misurare le distanze angolari, costituito di due bracci perpendicolari a croce, dei quali quello più grande, lungo un metro, veniva puntato verso la direzione del cielo da osservare ed era opportunamente graduato, mentre l’altro, più corto, scorreva sull’altro in modo da sottendere angoli maggiori (con il vertice sull’occhio e i lati passanti per gli estremi) all’aumentare della sua distanza dall’occhio dell’osservatore).
Nel 1569, all’età di 23 anni cominciò a fabbricarsi i propri strumenti da sé: cominciò con un sestante di raggio uguale a 1,5 metri, e successivamente con alcuni amici di Augusta iniziò la costruzione di un grande quadrante di 18 metri di raggio (che per essere collocato in posizione verticale richiedeva il lavoro di 20 uomini), resosi ben conto che la costruzione di strumenti di misura di grandi dimensione poteva far guadagnare notevolmente in precisione nelle misure di angoli.
Fu in quegli anni che dovette tornare a Knudstrup perché le condizioni di salute del padre si erano aggravate; e tuttavia non interruppe la sua attività. Iniziò subito, infatti la costruzione di un nuovo sestante a bracci molto lunghi, che utilizzò per effettuare misure posizionali di uno strano fenomeno celeste che scorse per la prima volta nella costellazione di Cassiopea la sera del 11 Novembre del 1572.
Tycho e la stella nova: i cieli non sono immutabili.
Quella sera Tycho, ospite dello zio Steen Bille alchimista, uscendo dal suo laboratorio, notò una stella luminosissima a nord-ovest di Cassiopea, più luminosa della stessa Venere. Fenomeni come questo erano stati osservati in passato; ne erano testimonianze soltanto le registrazioni molto dettagliate negli annali astronomici cinesi e le pitture murali di antiche culture americane. In Europa, al contrario, mancavano quasi completamente registrazioni storiche di stelle “novae” (nuove), come venivano chiamati questi fenomeni; la grande stella nova del 1054 d.C., prodotta dall’esplosione di una supernova (con questo termine viene indicata la fine esplosiva della vita di una stella di grande massa) che diede origine alla nebulosa Granchio, ad esempio, fu osservata nella costellazione del Toro ai primi di Luglio come una stella più luminosa della stella Venere e fu in congiunzione con la Luna (in fase di luna nuova) poco prima dell’alba il 5 o il 6 di Luglio, ma nonostante la sua visibilità nell’emisfero boreale, non esiste nessuna testimonianza nell’Europa del tempo di quello spettacolare evento astronomico.
Ciò si deve al fatto che nella visione cosmologica greca antica (che ebbe la sua espressione più completa nella cosmologia e nella fisica aristoteliche) al cielo erano assegnati natura divina e pertanto attributi di eternità e immutabilità. L’immutabilità del cielo era poi divenuta caratteristica sostanziale nella visione teologica dell’Universo nel Medioevo e quindi l’apparizione di una stella nova non poteva essere interpretata come un mutamento del cielo ma soltanto come un fenomeno prodotto all’interno delle sfere celesti (come i fulmini). La rivalutazione delle stelle novae come eventi celesti fu opera proprio di Tycho Brahe, che misurando le distanze nel cielo tra la stella nova che aveva osservato e le stelle della costellazione di Cassiopea per tutti i diciotto mesi in cui essa fu visibile, non ne rilevò alcuna variazione. Per realizzare queste misure utilizzò il sestante che aveva costruito in precedenza, di raggio uguale a 1,7 metri, appoggiandone un braccio al davanzale della finestra della sua stanza in posizione perfettamente orizzontale (la posizione orizzontale del braccio veniva verificata utilizzando un filo a piombo il quale doveva risultare allineato con una tacca dello stesso braccio opportunamente tracciata).
Il fatto che le distanze della stella nova dalle stelle di Cassiopea non avessero subito alcuna variazione provava l’appartenenza della stessa al cielo delle stelle fisse; ma Tycho (che pubblicò i risultati delle sue osservazioni nel resoconto “De nova et nullius aevi prius visa memoria”) non sfruttò la sua scoperta per mettere in discussione i principi fisici su cui si fondava la cosmologia geocentrica aristotelica, bensì si limitò a considerare l’evento un miracolo e, come tale, da accettare come evento assolutamente eccezionale, non inquadrabile in alcuno schema cosmologico (una stella nova non poteva essere indice della mutevolezza del Cielo, così come la resurrezione di Lazzaro non poteva essere considerata prova dell’immortalità dell’uomo).
Più tardi, nel 1577, e successivamente negli anni 1580, 1582 e 1585, Tycho osservò e misurò con estrema cura le posizioni di quattro comete. Se dopo l’osservazione della cometa del 1577 era giunto alla conclusione che essa doveva essere un oggetto celeste (quando confrontò i propri dati con quelli di altri astronomi che l’avevano osservata da località diverse, non notò alcuna parallasse) collocato ad oltre 230 raggi terrestri dalla Terra, quindi nella sfera di Venere del sistema tolemaico, dopo 10 anni, l’osservazione di tutte le comete ed il lavoro che vi dedicò lo condussero alla scelta di un modello cosmologico diverso da quello tolemaico, seppure non copernicano.
Il sistema tychonico
Dunque Tycho Brahe non fu favorevole al sistema copernicano.
Nonostante la grande precisione raggiunta dalle sue osservazioni (fu in grado di misurare angoli con una precisione di 2’ d’arco), non riuscì a misurare alcun movimento apparente delle stelle nel cielo (la “parallasse annua”) dovuta al moto di rivoluzione della Terra intorno al Sole teorizzato da Copernico; dal momento che assegnò alle stelle un diametro apparente uguale al minimo angolo misurabile, che egli aveva portato a 2’ d’arco, Tycho dedusse che se ci fosse stata una parallasse annua delle stelle essa sarebbe stata inferiore al diametro apparente delle stelle, e che quindi (poiché se più oggetti sono posti alla stessa distanza, a diametri maggiori corrispondono diametri angolari, o apparenti, maggiori) le stelle avrebbero avuto dimensioni lineari maggiori delle dimensioni dell’orbita terrestre copernicana. Naturalmente a Tycho sembrava assurdo concepire un universo nel quale gli astri avessero dimensioni maggiori delle loro distanze.
L’idea alternativa che concepì (il cosiddetto sistema “Tychonico”) prevedeva che la Terra fosse ancora immobile al centro dell’universo, ma che gli unici corpi celesti in moto di rivoluzione intorno ad essa fossero la Luna ed il Sole, ma che al contrario tutti i pianeti ruotassero intorno al Sole in modo tale che le orbite dei pianeti interni avessero raggio minore del raggio orbitale del Sole intorno alla Terra, mentre quello dei pianeti esterni doveva essere maggiore (perché essi potessero trovarsi all’opposizione, cioè dalla parte opposta del Sole rispetto alla Terra, sorgendo al tramonto del Sole e tramontando al sorgere del Sole, come in effetti fanno Marte, Giove e Saturno); Tycho pubblicò la sua teoria cosmologica nel 1588 nel trattato “De mundi aetherei recentioribus phaenomenis”. Il modello tychonico rappresenta un compromesso tra il geocentrismo e l’eliocentrismo; rispetto a quest’ultimo è più allineato alla tradizione, mantenendo valida l’ipotesi dell’immobilità e centralità della Terra, ma d’altra parte appare altrettanto incompatibile con la Fisica di Aristotele nel momento in cui pone i pianeti in rotazione intorno al Sole in modo assolutamente inconciliabile con l’idea aristotelica degli “orbi solidi” ( cioè delle sfere celesti cristalline concentriche alla Terra).
Va anche detto che, a dire il vero, la vera paternità del modello Tychonico è incerta; diversi documenti (la scoperta di annotazioni in diverse edizioni successive del “De Rivolutionibus”, che facevano riferimento al sistema Tychonico), ha prospettato la possibilità che il sistema di Tycho Brahe fosse nato da un’idea di Paul Wittich (1550 - 1587), giovane astronomo che egli ricevette ad Uraniborg nel 1580.
Più tardi, quando le complesse vicissitudini di una vita assai intensa indussero Tycho a trasferirsi a Praga, il matematico Nicolaus Reymarus Baer, detto “Ursus” (un autodidatta che era passato con uno studio tenace dai mestieri più umili, come quello di guardiano dei porci, all’incarico di matematico imperiale), ingaggiò con Tycho una feroce diatriba, rivendicando la paternità del suo modello cosmologico e accusandolo di plagio.
E tuttavia, al di là di tutte le discussioni suscitate dalla questione a quel tempo ed in seguito, non si può tralasciare che il modello cosmologico suddetto non fu altro che una versione più complicata di un’idea “base” che il pitagorico Eraclide Pontico aveva avuto duemila anni prima.
Quando Tycho lasciò Uraniborg per trasferirsi a Praga: incontro con Keplero e morte
Dopo la morte del suo re e mecenate Federico II nel 1588, Tycho entrò presto in conflitto con il suo successore Cristiano IV, il quale cominciò a togliergli le agevolazioni fiscali concessegli in precedenza, ritenendole privilegi eccessivi. Per questo motivo nel 1597, dopo venti anni a Hveen, egli decise di partire per il cuore dell’Europa, come altre volte aveva fatto in passato, certo che altrove, data la sua fama ormai consolidata di grande astronomo, avrebbe potuto lavorare in condizioni migliori.
«Gli astronomi devono essere cosmopoliti perché non ci si può attendere che uomini di stato ignoranti apprezzino i loro servigi»; con queste parole Tycho salutò amaramente Uraniborg mentre se ne andava portando con sé un imponente apparato comprendente, la sua biblioteca, i suoi uffici, la sua officina e buona parte dei suoi strumenti e con l’intenzione di farsi inviare successivamente quelli di dimensioni maggiori, quindi più difficili da trasportare.
Dopo due anni di viaggio attraverso la Germania, Tycho giunse nel 1599 a Praga e qui fu accolto con grandi onori dall’imperatore Rodolfo II, che non badò a spese pur di trattenerlo; anche se non lo nominò ufficialmente matematico di corte, forse anche per non contrariare l’allora matematico imperiale Nicolaus Baer, Rodolfo II lo considerò tale di fatto garantendogli un lauto stipendio oltre alla possibilità di scegliersi il luogo più adatto per l’installazione del suo osservatorio (Tycho scelse la collina di Benatek, a nord-est di Praga).
Nel frattempo la fama di grande matematico di un certo Keplero (latinizzazione del nome originale Kepler) si era diffusa in Europa al punto che Rodolfo II, mecenate delle scienze astronomiche, incurante del traballante bilancio del suo stato, alla morte di “Ursus” Baer (1600) pensò di offrire a Keplero l’incarico ufficiale di matematico imperiale, cosicché si trovò di fatto a retribuire due uomini per lo stesso incarico.
Così avvenne l’incontro tra Tycho e Keplero.
Entrambi avvertirono che quella era una grande possibilità; per Tycho era l’occasione di lavorare insieme ad un grande matematico e, anche grazie al lavoro di questi, di dare ancora più solidità e credibilità al suo modello cosmologico. Per Keplero fu l’occasione per lavorare in un grande osservatorio astronomico ed avere a disposizione una ingente quantità di dati sui quali poter continuare con maggior probabilità di successo la propria ricerca di un ordine matematico dell’Universo.
Keplero: gli studi
Johannes Kepler era nato a Weil der Stadt, cittadina sveva, nel 1571 (quando Tycho aveva già 25 anni e si costruiva da solo i propri strumenti); il nonno, ricco artigiano, era stato borgomastro della città, ma in seguito le fortune della famiglia erano declinate in seguito alla denuncia per stregoneria e alla condanna al rogo di una zia di Johannes. Il padre era poi un mercenario e, spesso lontano da casa, trascurò la famiglia; la madre Catherine Gundelmann, dal canto suo, fu accusata in età senile di commercio con il demonio e riuscì ad evitare il rogo in seguito all’intervento dello stesso Johannes, quando già era matematico e astronomo affermato.
Johannes, bambino di salute cagionevole e con un fastidioso difetto alla vista (che gli provocava talvolta uno sdoppiamento delle immagini), nonostante la povertà e le condizioni disastrate della famiglia ricevette una istruzione di ottimo livello per il solo fatto di essere nato nel Wurttenberg. Infatti l’affermazione del Luteranesimo in questa regione portò alla confisca dei conventi e dei monasteri cattolici da parte delle autorità. Dai beni immobili confiscati furono ricavate scuole primarie e secondarie che dovevano preparare i giovani all’accesso alle università di Wittenberg e Tubinga. I prìncipi sovvenzionavano un efficace sistema di incentivazione allo studio degli studenti meritevoli attraverso lo stanziamento di borse di studio (l’indipendenza dalla Chiesa di Roma doveva essere affermata potenziando il sistema di istruzione e di diffusione della cultura).
Keplero entrò a far parte della scuola elementare di Leoberg a sette anni nel 1578; successivamente nel 1584 entrò alla scuola di Grammatica di Adelberg, nel 1586 al seminario di Maulbronn e il 3 Settembre del 1589 si iscrisse ai corsi dell’Università di Tubinga per divenire “Magister Artium”. Due anni dopo, insieme al titolo, ottenne il diritto di studiare teologia; il corso dei suoi studi l’avrebbero condotto a divenire pastore luterano dottore in teologia se nel 1593, anno della morte di Georg Stadius, titolare della cattedra di Matematica presso la Stiffschule, a Graz, capitale degli stati della Stiria, quando le autorità stiriane chiesero all’Università di Tubinga il nome di un possibile sostituto, non fosse stato fatto il suo nome.
Keplero, che si era distinto durante i suoi studi universitari proprio per la sua abilità in matematica, quando gli fu comunicata la scelta ne fu entusiasta e partì subito a piedi per Graz, ove tenne la prima lezione il 24 Giugno del 1594. Il suo primo compenso fu, però, di soli 200 fiorini, con l’aggiunta di 20 fiorini per la formulazione di un calendario corredato di previsioni astrologiche per l’anno seguente. Occorre dire per la verità che la Matematica allora non era considerata una disciplina fondamentale tra le Scienze, le quali erano considerate campo di competenze anzitutto dei filosofi della Natura; essere docente di Matematica significava, oltre che insegnare gli scarni elementi allora noti (la Geometria euclidea piana e solida, l’Aritmetica ed un po’ di Algebra) era anche occuparsi di Astronomia, Astrologia nonché di aspetti cabalistici del linguaggio dei numeri e delle forme geometriche. Lo stipendio di Keplero dunque era misero e non gli bastava per vivere; per questo egli si convinse che il modo migliore per integrarlo era formulare oroscopi e previsioni astrologiche, attività molto redditizia in un’epoca dominata dall’ignoranza e dalla superstizione.
Il “Mysterium Cosmograficum”
L’insegnamento che Keplero aveva avuto a Tubinga nel campo dell’Astronomia da parte di Michael Maestlin (copernicano convinto) lo avevano convinto della veridicità dell’ipotesi di Copernico alimentando quell’interesse per l’astronomia che forse gli derivava dall’infanzia fin da quando, come compare in alcuni suoi scrupolosi appunti personali, la madre, dopo che egli a sei anni si era tolto da solo il primo dentino, lo portò con sé per premio su di una collina vicina ad osservare la splendida cometa apparsa nel 1577.
La motivazione di Keplero all’indagine cosmologica era di natura mistica; egli era convinto che attraverso di essa fosse possibile trovare una chiave geometrica dell’ordine cosmico, in particolare con lo studio del moto dei pianeti, proseguendo una linea tracciata nell’antichità da Pitagora e Platone. Da questa idea nacque il suo primo trattato di cosmologia: il “Mysterium Cosmograficum”.
In tutti i suoi scritti, a partire dal Mysterium, Keplero riportò tutto il suo percorso di studio e di ricerca, compresi gli errori più grossolani, e questo rende le sue opere di grande interesse storico, in quanto se ne può dedurre l’evoluzione del suo metodo di lavoro. E’ questo in effetti il principale motivo di interesse che si può trovare nel Mysterium, dato lo scarso valore scientifico del suo contenuto. Keplero infatti in esso voleva dimostrare che l’Universo era espressione della Gloria Divina e che le tre entità immobili dell’Universo (il Sole, le stelle fisse e lo spazio che li separa) erano in armonia con il mistero della Santissima Trinità, il quale naturalmente, essendo un mistero, come tale non poteva essere rivelato.
Keplero fornì un primo esempio della sua ricerca di una giustificazione geometrica dell’ordine universale mostrando come aveva inizialmente tentato di spiegare le dimensioni degli orbi inscrivendo dentro l’orbita di Saturno una successione di triangolazioni per individuale al loro interno l’orbita di Giove, quindi ripetendo l’operazione con una successione di quadrati per ricavare l’orbita di Marte e così via...
A questo primo fallimento seguì un secondo tentativo con il quale Keplero provò a inscrivere tra i sei orbi dei pianeti (compresa la Terra) i cinque poliedri regolari in modo che ognuno, inscritto nella sfera esterna ad esso, fosse circoscritto a quella più interna. Questo avrebbe spiegato anche il motivo della presenza di sei orbi planetari nell’Universo (immaginate quale sarebbe stata la delusione di Keplero se qualche astronomo suo contemporaneo avesse scoperto Urano aumentando così il numero di orbi celesti).
L’incontro con Tycho: la “Astronomia nova”
Quando Tycho incontrò Keplero, il suo gruppo di ricerca a Praga era alle prese con il grosso problema di trovare una descrizione credibile del moto di Marte: oggi sappiamo che Marte ha un’orbita particolarmente eccentrica, e questo spiega perché all’epoca neanche le previsioni basate sul modello copernicano (che prevedeva per i pianeti orbite circolari) erano confermate dalle osservazioni. Tycho assegnò a Keplero, fin dai primi tempi in cui cominciò a far parte dei suoi collaboratori, il compito di studiare il moto di Marte, di cui fino ad allora si era occupato Christen Soerensen con scarso successo.
Prima di morire (nell’ottobre 1601) Tycho cercò in ogni modo di convincere Keplero a dedicarsi con il massimo impegno alle osservazioni, e a tentare di dimostrare attraverso di esse la validità del modello cosmologico in cui credeva.
Keplero iniziò ad analizzare con molto rigore i dati posizionali di Marte, cominciando a individuare le opposizioni successive di Marte (si avvalse in ciò di dati raccolti in diverse tavole astronomiche, e soprattutto delle osservazioni di Tycho a Praga) per ricavare dai loro tempi e dalle loro posizioni sullo zodiaco, indicazioni sull’orbita. Ma ben presto comprese che non avrebbe potuto ottenere risultati soddisfacenti se non fosse riuscito prima a trovare un modello valido per il moto della Terra intorno al Sole. Così cercò di trovare tre posizioni di Marte nel cielo corrispondenti ad istanti nei quali esso si trovava nello stesso punto dell’orbita, avendo dedotto che in tal modo sarebbe stato possibile individuare con certezza l’orbita della Terra per via geometrica e trigonometrica, verificando poi il modello ottenuto con osservazioni ulteriori.
Ottenuta una credibile teoria del moto della Terra Keplero tuttavia non tornò ad occuparsi subito di Marte, ma per qualche tempo si dedicò all’interpretazione dinamica dei moti; bisogna dire subito che la dinamica kepleriana non ha avuto grande successo. Le sue affermazioni furono grossolane e inesatte e risentivano ancora dell’influenza della Fisica di Aristotele.
Per Keplero il Sole era responsabile della forza che guidava i pianeti nel loro moto intorno ad esso, ma le forze agenti su di essi erano direttamente proporzionali alle rispettive velocità. E tuttavia anche questa affermazione non corretta contribuì a metterlo sulla strada giusta nella formulazione delle sue leggi del moto dei pianeti.
Quando, nel 1602, ritornò allo studio del moto di Marte, dai suoi studi sul moto della Terra intorno al Sole aveva tratto una relazione di proporzionalità inversa tra la velocità e la distanza dal Sole, verificata all’apogeo e al perigeo (esiste ad esempio una differenza di circa tre giorni tra la durata del ciclo delle fasi lunari con la Terra all’afelio e quella con la Terra al perielio, dovuta al fatto che la velocità della Terra intorno al Sole varia con la distanza; per lo stesso motivo la durata del giorno solare varia nel corso dell’anno). Supponendo che la forza agente sul pianeta fosse direttamente proporzionale alla velocità, Keplero ne ricavò una legge errata, secondo la quale la forza gravitazionale agente sui pianeti era inversamente proporzionale alla distanza (diversa da quella che poi Newton avrebbe ricavato). Tuttavia, al di là delle conclusioni errate della dinamica kepleriana, il suggerimento della relazione esistente tra velocità e distanza fu prezioso per i successivi sviluppi della teoria del moto di Marte, ed altrettanto determinante fu lo stato d’animo di Keplero, ormai pessimista, dopo due anni di calcoli, sulle possibilità di poter attribuire a Marte un’orbita circolare.
Così Keplero cominciò a cercare di deformare la traiettoria utilizzando epicicli che ne producessero una ovalizzazione; gli esiti negativi ottenuti lo condussero a provare se fosse possibile ottenerne di migliori ipotizzando la forma ellittica per l’orbita di Marte: i risultati furono allora sorprendentemente i migliori tra tutti quelli precedenti.
Nel trattato “Astronomia nova” (sottotitolato “De motibus stella Martis”), pubblicato nel 1609, Keplero pubblicò i suoi risultati ottenuti per l’orbita di Marte, estendendo poi a tutto il sistema solare il modello di orbita ellittica con velocità dipendente dalla distanza dal pianeta. Le conclusioni di Keplero sono oggi valide con un buon grado di approssimazione e sono tuttora studiate come le prime due leggi di Keplero:
(I) le orbite dei pianeti sono ellittiche ed il Sole occupa uno dei due fuochi di ogni ellisse,
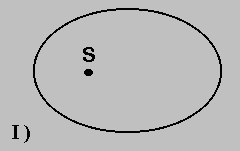
(II) la velocità areolare, cioè l’area descritta dal raggio-vettore che collega il Sole ad un pianeta nell’unità di tempo, è costante. In altre parole, poiché una qualsiasi area descritta dal raggio-vettore del pianeta è proporzionale al prodotto della distanza per la lunghezza dell’arco, all’aumentare della distanza diminuisce l’arco percorso in uno stesso tempo, quindi diminuisce la velocità del pianeta (nella figura sottostante i raggi vettori sono i segmenti SP e SP’ e gli archi descritti dal pianeta sono gli archi di ellisse PP’, mentre le aree descritte, o “spazzate” dal raggio vettore durante il moto del pianeta in uno stesso intervallo di tempo, sono quelle riempite).
In base alla seconda legge la velocità di un pianeta al perielio, è dunque superiore a quella all’afelio.
I carteggio con Galileo e il cannocchiale
Nel frattempo, nel settembre del 1609, Galileo realizzò il suo prototipo di cannocchiale e pensò subito di osservare con esso il cielo notturno.
Quando nel 1610 Galileo pubblicò un resoconto delle sue prime osservazioni con lo strumento ottico, nel “Sidereus Nuncius”, Keplero, che ne ricevette una copia dall’ambasciatore fiorentino Giuliano de’ Medici, mostrò grande entusiasmo per il lavoro di Galileo e gli inviò la sua personale richiesta di poter ricevere un esemplare del telescopio galileiano e verificare la validità delle osservazioni fatte da Galileo.
Galileo si scusò di non potergli inviare il suo, che aveva 20 ingrandimenti (Keplero aveva costruito per conto suo un cannocchiale che, utilizzando due lenti biconvesse anziché una biconvessa ed una biconcava, la soluzione migliore trovata da Galileo, non riusciva ad andare oltre i 10 ingrandimenti) perché ne aveva fatto dono al granduca di Toscana Cosimo II, ma gli promise di adoperarsi per costruirgliene uno. Galileo non fece menzione direttamente a Keplero della sua nuova scoperta, quella della forma allungata di Saturno, la cui figura vista al telescopio non aveva la forma semplice di un piccolo disco, come accadeva per gli altri pianeti, ma appariva allungata, come se fosse munita di due lobi laterali, o attorniata da due satelliti molto vicini, l’uno dalla parte opposta dell’altro.
Tuttavia alla risposta a Keplero Galileo
allegò una lunga sequenza di lettere dell’alfabeto,
apparentemente senza nessun senso, ma che opportunamente
anagrammate rivelavano la frase “Altissimum planetam
tergerminum observavi” (“ho visto il pianeta più
alto”, Saturno, il pianeta più lontano tra quelli visibili
ad occhio nudo, “formato di tre parti”).
Pur se Keplero si dilettava di enigmistica, la risoluzione
dell’anagramma fu assolutamente impossibile per lui.
Altrettanto difficile gli fu poi la decifrazione di un altro anagramma consegnato da Galileo all’ambasciatore Giuliano de’ Medici perché lo facesse recapitare allo stesso Keplero, “Haec immatura a me iam frustra leguntur”, frase con senso compiuto che anagrammata avrebbe dovuto trasformarsi nel verso “Cynthiae figuras aemulatur Mater amorum”, “la dea madre dell’amore (Venere) imita le forme di Cynthia (la Luna)”, verso che annunciava un’altra grande scoperta che, nel dibattito tra fautori di diversi sistemi cosmologici, poteva rafforzare ulteriormente la posizione di coloro che erano favorevoli sia al modello di Tycho Brahe che a coloro che sostenevano la validità dell’ipotesi eliocentrica copernicana.
Alla fine dell’estate del 1610 finalmente Keplero poté utilizzare un cannocchiale galileiano, prestatogli dal duca di Baviera, il quale lo aveva avuto in dono dallo stesso Galileo, e vi poté finalmente osservare i “pianeti medicei”, come Galileo aveva chiamato i satelliti di Giove (fu proprio Keplero a chiamarli per primo “satelliti”, dal latino “satellites” che significa guardie).
Successivamente Keplero spiegò teoricamente il funzionamento del cannocchiale nel trattato di ottica dal titolo “Dioptrice”, pubblicato ad Augusta nel 1611.
“Harmonices Mundi” e la terza legge di Keplero
Negli anni successivi Keplero, dopo aver visto morire in poco tempo il figlio Federico, la prima moglie Barbara e il suo mecenate Rodolfo II, si trasferì a Linz, ospitatovi dall’imperatore Mattia. Là (ove si costruì una nuova famiglia risposandosi) si dedicò di nuovo a speculazioni teorico-mistiche della stessa natura di quelle che avevano portato al Mysterium.
La ricerca di un ordine matematico dell’Universo come espressione divina lo portò nel 1619 a realizzare l’opera “Harmonices mundi”: in essa Keplero giunse finalmente a definire quella legge matematica che doveva descrivere i moti dei pianeti intorno al Sole e che aveva cercato lungamente. Essa è oggi nota come la terza legge di Keplero:
(III) i cubi dei semiassi maggiori di ogni pianeta sono direttamente proporzionali ai rispettivi periodi di rivoluzione
A3
————— = k
T2
dove k è la cosiddetta “costante di Keplero”.
Negli anni seguenti Keplero ultimò il trattato “Epitome astronomiae copernicanae”, un compendio astronomico di nome, ma di fatto un ampio saggio scientifico che, oltre a fare il punto delle conoscenze astronomiche dell’epoca, si offriva agli studenti universitari come un testo completo e approfondito, e pubblicò successivamente (1624) le “Tabulae Rudolphine”, contenenti le previsioni astronomiche sul moto dei pianeti dedotte in base alle sue nuove leggi.
Così Keplero, completava la sua grande produzione scientifica, risultato di un lavoro proseguito incessantemente per tanti anni nonostante le avversità della vita non gli dessero tregua; l’accusa per stregoneria dell’anziana madre aveva reso necessario un suo precipitoso ritorno a casa mentre era ancora a Linz.
Successivamente quando pubblicò le Tavole Rudolphinae e ne offrì una copia all’imperatore Ferdinando, successore di Mattia, ottenne in cambio la promessa di una importante carica a Praga, ma soltanto a patto che si fosse convertito al cattolicesimo; naturalmente Keplero si rifiutò e si dovette rimettere in viaggio nel 1627.
Fu accolto presso la corte di Zagan in Slesia e vi rimase per qualche tempo finché alfine decise di recarsi a Ratisbona per riscuotere una somma in denaro che l’imperatore Ferdinando, insediatosi a Ratisbona in quegli anni, gli doveva. Ma ormai stremato dai continui viaggi e dalle vicissitudini drammatiche della sua vita, appena giunto, a Ratisbona, si ammalò e morì il 5 Novembre 1630.
Conclusioni
Meno di tre anni dopo la morte di Keplero, Galileo fu costretto a comparire davanti al Tribunale della Santa Inquisizione con l’accusa di eresia per aver sostenuto in un suo scritto (il “Dialogo sul flusso e reflusso delle maree”) argomenti contrari alla cosmologia geocentrica, e quindi alle Sacre Scritture, che i teologi ritenevano in accordo soltanto con essa.
Gli fu risparmiata la vita (a lui uomo di scienza noto e apprezzato) soltanto perché, dopo mesi di segregazione e tortura, accettò di abiurare le sue tesi.
Fu per lui, ormai vecchio e stanco, una umiliazione grande e inaspettata, dopo una vita dedicata alla ricerca a costo della sua stessa salute, e soprattutto dopo che era lodato e apprezzato presso altolocati rappresentanti della stessa Chiesa di Roma. Ma quell’atto impositivo da parte di un’istituzione che voleva affermare la propria autorità in un terreno che non era il suo e intorno alla quale brillavano di luce riflessa accademici ignoranti, in realtà era già il segno di una resa inevitabile: la resa di un mondo che vedeva crollare le proprie primitive certezze di fronte all’urto delle nuove idee nate dal lavoro tenace di uomini lungimiranti e coraggiosi, che la storia fortunatamente ha ricompensato in onori e gloria più della loro vita.
Bibliografia:
J.P. Vertet: Storia dell’Astronomia, Ed. Longanesi
Da “Astronomia: alla scoperta del cielo” (Vol. 5, pp.1814-1821)
Kuhn: La rivoluzione copernicana, Ed. Einaudi (PBE)
Monografia n.43-2000/2
Torna alla Home Page di Testi & Trattati